

 ในชีวิตประจำวันทุกคนต้องเคยพบกับปัญหาต่างๆ ไม่ว่าจะเป็นปัญหาด้านการเรียน การงาน การเงินหรือแม้แต่การเล่นเกม เมื่อพบกับปัญหาแต่ละคนมีวิธีการที่จะจัดการหรือแก้ปัญหาเหล่านั้นแตกต่างกันไป ซึ่งแต่ละวิธีการอาจให้ผลลัพธ์ที่เหมือนหรือแตกต่างกันเล็กน้อย ทั้งนี้ขึ้นอยู่กับความรู้ ความสามารถ และประสบการณ์ของบุคคลนั้น อย่างไรก็ตามหากเรานำวิธีการแก้ปัญหาต่างๆนั้นมาวิเคราะห์ให้ดี จะพบว่าวิธีการเหล่านั้นเป็นทฤษฎีซึ่งมีรูปแบบที่แน่นอนได้ และบางครั้งต้องอาศัยการเรียนรู้ในระดับสูงเพื่อแก้ปัญหาบางอย่างให้สมบูรณ์แบบ แต่ก่อนที่เราจะศึกษาต่อไป ลองพิจารณาปัญหาเหล่านี้ ในชีวิตประจำวันทุกคนต้องเคยพบกับปัญหาต่างๆ ไม่ว่าจะเป็นปัญหาด้านการเรียน การงาน การเงินหรือแม้แต่การเล่นเกม เมื่อพบกับปัญหาแต่ละคนมีวิธีการที่จะจัดการหรือแก้ปัญหาเหล่านั้นแตกต่างกันไป ซึ่งแต่ละวิธีการอาจให้ผลลัพธ์ที่เหมือนหรือแตกต่างกันเล็กน้อย ทั้งนี้ขึ้นอยู่กับความรู้ ความสามารถ และประสบการณ์ของบุคคลนั้น อย่างไรก็ตามหากเรานำวิธีการแก้ปัญหาต่างๆนั้นมาวิเคราะห์ให้ดี จะพบว่าวิธีการเหล่านั้นเป็นทฤษฎีซึ่งมีรูปแบบที่แน่นอนได้ และบางครั้งต้องอาศัยการเรียนรู้ในระดับสูงเพื่อแก้ปัญหาบางอย่างให้สมบูรณ์แบบ แต่ก่อนที่เราจะศึกษาต่อไป ลองพิจารณาปัญหาเหล่านี้
 ตัวอย่างที่ 1.1 เกมทายใจ คือ เกมให้ผู้เล่นทายตัวเลข 3 ตัว ในการเล่นเกมต้องใช้ผู้เล่น 2 คน คนที่หนึ่ง คือ ผู้กำหนด เป็นคนกำหนดเลข 3 ตัว ที่ไม่ซ้ำกันโดยเลือกจากกลุ่มตัวเลข 1-9 และอีกคนหนึ่งคือ ผู้ทาย เป็นผู้ทายเลข 3 ตัว ที่ไม่ซ้ำกัน ที่ผู้กำหนดได้กำหนดเอาไว้แล้ว หลังจากที่ผู้ทายทายเลขแต่ละครั้ง ผู้กำหนดต้องให้รายละเอียดว่าตัวเลขที่ทายมานั้นถูกต้องกี่ตัว และในกรณีที่ตัวเลขที่ทายมาถูกตำแหน่งด้วยก็ต้องบอกว่าถูกตำแหน่งกี่ตัว เช่น ถ้าตัวเลขที่กำหนดไว้เป็น 815 และ ผู้ทายทายว่า 123 ผู้กำหนดต้องแจ้งว่าตัวเลขที่ทายนั้นถูก 1 ตัว และไม่มีตัวใดถูกตำแหน่ง ดังรูป เป็นตารางแสดงข้อมูลการเล่นเกมทายใจ ตัวอย่างที่ 1.1 เกมทายใจ คือ เกมให้ผู้เล่นทายตัวเลข 3 ตัว ในการเล่นเกมต้องใช้ผู้เล่น 2 คน คนที่หนึ่ง คือ ผู้กำหนด เป็นคนกำหนดเลข 3 ตัว ที่ไม่ซ้ำกันโดยเลือกจากกลุ่มตัวเลข 1-9 และอีกคนหนึ่งคือ ผู้ทาย เป็นผู้ทายเลข 3 ตัว ที่ไม่ซ้ำกัน ที่ผู้กำหนดได้กำหนดเอาไว้แล้ว หลังจากที่ผู้ทายทายเลขแต่ละครั้ง ผู้กำหนดต้องให้รายละเอียดว่าตัวเลขที่ทายมานั้นถูกต้องกี่ตัว และในกรณีที่ตัวเลขที่ทายมาถูกตำแหน่งด้วยก็ต้องบอกว่าถูกตำแหน่งกี่ตัว เช่น ถ้าตัวเลขที่กำหนดไว้เป็น 815 และ ผู้ทายทายว่า 123 ผู้กำหนดต้องแจ้งว่าตัวเลขที่ทายนั้นถูก 1 ตัว และไม่มีตัวใดถูกตำแหน่ง ดังรูป เป็นตารางแสดงข้อมูลการเล่นเกมทายใจ

 จะเห็นว่าการแก้ปัญหาดังกล่าวข้างต้น นอกจากจะใช้วิธีลองผิดลองถูกในการทายครั้งแรกๆ แล้วยังมีการใช้เหตุผลประกอบการแก้ปัญหาซึ่งเราเรียกวิธีการดังกล่าวว่า "วิธีขจัด" (Method of elimination) กล่าวคือ จะแยกข้อมูลกรณีที่เป็นไปไม่ได้ทิ้ง จนเหลือกรณีที่เป็นไปได้ วิธีการดังกล่าวสามารถอธิบายได้ ว่าทำไมจึงคิดเช่นนั้น รูปแบบของการใช้เหตุผลประกอบการแก้ปัญหาอาจแตกต่างกันขึ้นอยู่กับเงื่อนไข ในปัญหาบางปัญหาอาจจะขจัด ให้เหลือกรณีเดียวไม่ได้แต่อาจจะทำเหลือกรณีน้อยที่สุด จะเห็นว่าการแก้ปัญหาดังกล่าวข้างต้น นอกจากจะใช้วิธีลองผิดลองถูกในการทายครั้งแรกๆ แล้วยังมีการใช้เหตุผลประกอบการแก้ปัญหาซึ่งเราเรียกวิธีการดังกล่าวว่า "วิธีขจัด" (Method of elimination) กล่าวคือ จะแยกข้อมูลกรณีที่เป็นไปไม่ได้ทิ้ง จนเหลือกรณีที่เป็นไปได้ วิธีการดังกล่าวสามารถอธิบายได้ ว่าทำไมจึงคิดเช่นนั้น รูปแบบของการใช้เหตุผลประกอบการแก้ปัญหาอาจแตกต่างกันขึ้นอยู่กับเงื่อนไข ในปัญหาบางปัญหาอาจจะขจัด ให้เหลือกรณีเดียวไม่ได้แต่อาจจะทำเหลือกรณีน้อยที่สุด
 นอกจากวิธีการแก้ปัญหาที่ยกตัวอย่างมาซึ่งได้แก่ วิธีการลองผิดลองถูก การใช้เหตุผล การใช้วิธีขจัด ยังมีวิธีการแก้ปัญหาอีกมากมายที่ผู้แก้ปัญหาสามารถเลือกใช้ให้เข้ากับตัวปัญหาและประสบการณ์ของผู้แก้ปัญหาเอง แต่อย่างไรก็ตาม วิธีการเหล่านี้ล้วนมีขั้นตอนที่คล้ายคลึงกัน และจากการศึกษาพฤติกรรมในการเรียนรู้และแก้ปัญหาของมนุษย์พบว่าโดยปกติมนุษย์มีกระบวนการในการแก้ปัญหาประกอบด้วย 4 ขั้นตอนดังรูป นอกจากวิธีการแก้ปัญหาที่ยกตัวอย่างมาซึ่งได้แก่ วิธีการลองผิดลองถูก การใช้เหตุผล การใช้วิธีขจัด ยังมีวิธีการแก้ปัญหาอีกมากมายที่ผู้แก้ปัญหาสามารถเลือกใช้ให้เข้ากับตัวปัญหาและประสบการณ์ของผู้แก้ปัญหาเอง แต่อย่างไรก็ตาม วิธีการเหล่านี้ล้วนมีขั้นตอนที่คล้ายคลึงกัน และจากการศึกษาพฤติกรรมในการเรียนรู้และแก้ปัญหาของมนุษย์พบว่าโดยปกติมนุษย์มีกระบวนการในการแก้ปัญหาประกอบด้วย 4 ขั้นตอนดังรูป

 1. การวิเคราะห์และกำหนดรายละเอียดของปัญหา 1. การวิเคราะห์และกำหนดรายละเอียดของปัญหา
การวิเคราะห์และกำหนดรายละเอียดของปัญหา(State the problem) ขั้นตอนนี้เป็นขั้นตอนแรกสุดก่อนที่จะลงมือแก้ปัญหา แต่ผู้แก้ปัญหามักจะมองข้ามความสำคัญของขั้นตอนนี้อยู่เสมอ จุดประสงค์ของขั้นตอนนี้ คือ การทำความเข้าใจกับปัญหาเพื่อแยกให้ออกว่าข้อมูลที่กำหนดมาในปัญหาหรือเงื่อนไขของปัญหาคืออะไร และสิ่งที่ต้องการคืออะไร อีกทั้งวิธีการที่ใช้ประมวลผล ในการวิเคราะห์ปัญหา กล่าวสรุปมีองค์ประกอบในการวิเคราะห์ดังนี้
 การระบุข้อมูลเข้า ได้แก่ การพิจารณาข้อมูลและเงื่อนไขที่กำหนดมาในปัญหา การระบุข้อมูลเข้า ได้แก่ การพิจารณาข้อมูลและเงื่อนไขที่กำหนดมาในปัญหา
 การระบุข้อมูลออก ได้แก่ การพิจารณาเป้าหมายหรือสิ่งที่ต้องการหาคำตอบ การระบุข้อมูลออก ได้แก่ การพิจารณาเป้าหมายหรือสิ่งที่ต้องการหาคำตอบ
 การกำหนดวิธีประมวลผล ได้แก่ การพิจารณาขั้นตอนวิธีการได้มาซึ่งคำตอบหรือข้อมูลออก การกำหนดวิธีประมวลผล ได้แก่ การพิจารณาขั้นตอนวิธีการได้มาซึ่งคำตอบหรือข้อมูลออก
 ตัวอย่างที่ 1.2 แสดงวิธีการวิเคราะห์และกำหนดรายละเอียดของการหาค่าเฉลี่ยของจำนวนเต็ม 5 จำนวน ได้แก่ 0 3 4 8 และ 12 ตัวอย่างที่ 1.2 แสดงวิธีการวิเคราะห์และกำหนดรายละเอียดของการหาค่าเฉลี่ยของจำนวนเต็ม 5 จำนวน ได้แก่ 0 3 4 8 และ 12

 ตัวอย่างที่ 1.3 แสดงการวิเคราะห์และกำหนดรายละเอียดของการหาค่า x เมื่อ x คือจำนวนเต็มจำนวนหนึ่งในกลุ่มของจำนวนเต็ม 5 จำนวน ที่มีค่าเฉลี่ยเป็น 10 และอีก 4 จำนวน ได้แก่ 3 4 8 และ 12 ตัวอย่างที่ 1.3 แสดงการวิเคราะห์และกำหนดรายละเอียดของการหาค่า x เมื่อ x คือจำนวนเต็มจำนวนหนึ่งในกลุ่มของจำนวนเต็ม 5 จำนวน ที่มีค่าเฉลี่ยเป็น 10 และอีก 4 จำนวน ได้แก่ 3 4 8 และ 12

2. การเลือกเครื่องมือและการออกแบบขั้นตอนวิธี
 การเลือกเครื่องมือและการออกแบบขั้นตอนวิธี (Tool and Algorithm development) ขั้นตอนนี้เป็นขั้นตอนของการวางแผนในการแก้ปัญหาอย่างละเอียดถี่ถ้วน หลังจากที่เราทำความเข้าใจกับปัญหา พิจารณาข้อมูลและเงื่อนไขที่มีอยู่ และสิ่งที่เราต้องการหาในขั้นตอนที่ 1 แล้ว เราสามารถคาดคะเนวิธีการที่จะใช้ในการแก้ปัญหา ขั้นตอนนี้จำเป็นต้องอาศัยประสบการณ์ของผู้แก้ปัญหาเป็นหลัก หากผู้แก้ปัญหาเคยพบกับปัญหาทำนองนี้มาแล้วก็สามารถดำเนินการตามแนวทางที่เคยปฏิบัติมา การเลือกเครื่องมือและการออกแบบขั้นตอนวิธี (Tool and Algorithm development) ขั้นตอนนี้เป็นขั้นตอนของการวางแผนในการแก้ปัญหาอย่างละเอียดถี่ถ้วน หลังจากที่เราทำความเข้าใจกับปัญหา พิจารณาข้อมูลและเงื่อนไขที่มีอยู่ และสิ่งที่เราต้องการหาในขั้นตอนที่ 1 แล้ว เราสามารถคาดคะเนวิธีการที่จะใช้ในการแก้ปัญหา ขั้นตอนนี้จำเป็นต้องอาศัยประสบการณ์ของผู้แก้ปัญหาเป็นหลัก หากผู้แก้ปัญหาเคยพบกับปัญหาทำนองนี้มาแล้วก็สามารถดำเนินการตามแนวทางที่เคยปฏิบัติมา
 ขั้นตอนนี้จะเริ่มจากการเลือกเครื่องมือที่ใช้ในการแก้ปัญหา โดยพิจารณาความเหมาะสมระหว่างเครื่องมือกับเงื่อนไขต่างๆ ของปัญหาซึ่งหมายรวมถึงความสามารถของเครื่องมือในการแก้ปัญหาดังกล่าว และสิ่งที่สำคัญคือความคุ้นเคยในการใช้งานเครื่องมือนั้นๆ ของผู้แก้ปัญหาสำคัญคือความคุ้นเคยในการใช้งานเครื่องมือนั้นๆ ของผู้แก้ปัญหา ขั้นตอนนี้จะเริ่มจากการเลือกเครื่องมือที่ใช้ในการแก้ปัญหา โดยพิจารณาความเหมาะสมระหว่างเครื่องมือกับเงื่อนไขต่างๆ ของปัญหาซึ่งหมายรวมถึงความสามารถของเครื่องมือในการแก้ปัญหาดังกล่าว และสิ่งที่สำคัญคือความคุ้นเคยในการใช้งานเครื่องมือนั้นๆ ของผู้แก้ปัญหาสำคัญคือความคุ้นเคยในการใช้งานเครื่องมือนั้นๆ ของผู้แก้ปัญหา
 อีกสิ่งหนึ่งที่สำคัญในการแก้ปัญหา คือ ยุทธวิธีที่ใช้ในการแก้ปัญหาหรือที่เรียกว่า ขั้นตอนวิธี(Algorithm) ในการแก้ปัญหา หลังจากที่เราได้เครื่องมือช่วยแก้ปัญหาแล้วผู้แก้ปัญหาต้องวางแผนว่าจะใช้เครื่องมือดังกล่าวเพื่อให้ได้ผลลัพธ์ที่ถูกต้องและดีที่สุด การออกแบบขั้นตอนวิธีในการแก้ปัญหา ผู้แก้ปัญหาควรใช้แผนภาพหรือเครื่องมือในการแสดงขั้นตอนการทำงานเพื่อให้ง่ายต่อความเข้าใจ เช่น ผังงาน(Flowchart) ที่จำลองขั้นตอนวิธีในการแก้ปัญหาในรูปสัญลักษณ์ รหัสลำลองหรือรหัสเทียม (pseudo code) ซึ่งเป็นการจำลองขั้นตอนวิธีของการแก้ปัญหาในรูปของคำบรรยาย การใช้เครื่องมือช่วยออกแบบดังกล่าวนอกจากแสดงกระบวนการที่ชัดเจนแล้ว ยังช่วยให้ผู้แก้ปัญหาสามารถหาข้อผิดพลาดของวิธีการที่ใช้ได้ง่ายและแก้ไขได้อย่างรวดเร็ว อีกสิ่งหนึ่งที่สำคัญในการแก้ปัญหา คือ ยุทธวิธีที่ใช้ในการแก้ปัญหาหรือที่เรียกว่า ขั้นตอนวิธี(Algorithm) ในการแก้ปัญหา หลังจากที่เราได้เครื่องมือช่วยแก้ปัญหาแล้วผู้แก้ปัญหาต้องวางแผนว่าจะใช้เครื่องมือดังกล่าวเพื่อให้ได้ผลลัพธ์ที่ถูกต้องและดีที่สุด การออกแบบขั้นตอนวิธีในการแก้ปัญหา ผู้แก้ปัญหาควรใช้แผนภาพหรือเครื่องมือในการแสดงขั้นตอนการทำงานเพื่อให้ง่ายต่อความเข้าใจ เช่น ผังงาน(Flowchart) ที่จำลองขั้นตอนวิธีในการแก้ปัญหาในรูปสัญลักษณ์ รหัสลำลองหรือรหัสเทียม (pseudo code) ซึ่งเป็นการจำลองขั้นตอนวิธีของการแก้ปัญหาในรูปของคำบรรยาย การใช้เครื่องมือช่วยออกแบบดังกล่าวนอกจากแสดงกระบวนการที่ชัดเจนแล้ว ยังช่วยให้ผู้แก้ปัญหาสามารถหาข้อผิดพลาดของวิธีการที่ใช้ได้ง่ายและแก้ไขได้อย่างรวดเร็ว
3. การดำเนินการแก้ปัญหา
 การดำเนินการแก้ปัญหา(Implementation) หลังจากที่ได้ออกแบบขั้นตอนวิธีเรียบร้อยแล้ว ขั้นตอนนี้เป็นขั้นตอนที่ต้องลงมือแก้ปัญหาโดยใช้เครื่องมือที่ได้เลือกไว้ หากการแก้ปัญหาดังกล่าวใช้คอมพิวเตอร์เข้ามาช่วยงาน ขั้นตอนนี้ก็เป็นการใช้งานโปรแกรมสำเร็จหรือใช้ภาษาคอมพิวเตอร์เขียนโปรแกรมแก้ปัญหา ขั้นตอนนี้ต้องอาศัยความรู้เกี่ยวกับเครื่องมือที่เลือกใช้ซึ่งผู้แก้ปัญหาต้องศึกษาให้เข้าใจและเชี่ยวชาญ ในขณะที่ดำเนินการหากพบแนวทางที่ดีกว่าที่ออกแบบไว้ก็สามารถปรับเปลี่ยนได้ การดำเนินการแก้ปัญหา(Implementation) หลังจากที่ได้ออกแบบขั้นตอนวิธีเรียบร้อยแล้ว ขั้นตอนนี้เป็นขั้นตอนที่ต้องลงมือแก้ปัญหาโดยใช้เครื่องมือที่ได้เลือกไว้ หากการแก้ปัญหาดังกล่าวใช้คอมพิวเตอร์เข้ามาช่วยงาน ขั้นตอนนี้ก็เป็นการใช้งานโปรแกรมสำเร็จหรือใช้ภาษาคอมพิวเตอร์เขียนโปรแกรมแก้ปัญหา ขั้นตอนนี้ต้องอาศัยความรู้เกี่ยวกับเครื่องมือที่เลือกใช้ซึ่งผู้แก้ปัญหาต้องศึกษาให้เข้าใจและเชี่ยวชาญ ในขณะที่ดำเนินการหากพบแนวทางที่ดีกว่าที่ออกแบบไว้ก็สามารถปรับเปลี่ยนได้
4. การตรวจสอบและปรับปรุง
 การตรวจสอบและปรับปรุง(Refinement) หลังจากที่ลงมือแก้ปัญหาแล้วต้องตรวจสอบให้แน่ใจว่าวิธีการนี้ให้ผลลัพธ์ที่ถูกต้อง โดยผู้แก้ปัญหาต้องตรวจสอบว่าขั้นตอนวิธีที่สร้างขึ้นสอดคล้องกับรายละเอียดของปัญหา ซึ่งได้แก่ ข้อมูลเข้า และข้อมูลออก เพื่อให้มั่นใจว่าสามารถรองรับข้อมูลเข้าได้ในทุกกรณีอย่างถูกต้องและสมบูรณ์ ในขณะเดียวกันก็ต้องปรับปรุงวิธีการเพื่อให้การแก้ปัญหานี้ได้ผลลัพธ์ที่ดีที่สุด การตรวจสอบและปรับปรุง(Refinement) หลังจากที่ลงมือแก้ปัญหาแล้วต้องตรวจสอบให้แน่ใจว่าวิธีการนี้ให้ผลลัพธ์ที่ถูกต้อง โดยผู้แก้ปัญหาต้องตรวจสอบว่าขั้นตอนวิธีที่สร้างขึ้นสอดคล้องกับรายละเอียดของปัญหา ซึ่งได้แก่ ข้อมูลเข้า และข้อมูลออก เพื่อให้มั่นใจว่าสามารถรองรับข้อมูลเข้าได้ในทุกกรณีอย่างถูกต้องและสมบูรณ์ ในขณะเดียวกันก็ต้องปรับปรุงวิธีการเพื่อให้การแก้ปัญหานี้ได้ผลลัพธ์ที่ดีที่สุด
ขั้นตอนทั้ง 4 ขั้นตอนดังกล่าวข้างต้น เป็นเสมือนขั้นบันได (stair) ที่ทำให้มนุษย์สามารถประสบความสำเร็จในการแก้ปัญหาต่างๆได้ รวมทั้งการเขียนหรือพัฒนาโปรแกรมคอมพิวเตอร์เพื่อแก้ปัญหาก็ต้องใช้กระบวนการตามขั้นตอนทั้ง 4 นี้เช่นกัน

 ขั้นตอนที่สำคัญในการแก้ปัญหา คือ การวางแผน การวางแผนที่ดีจะช่วยให้แก้ปัญหาเป็นไปได้โดยง่าย ผู้ที่สามารถวางแผนในการแก้ปัญหาได้ดีนอกจากจะต้องใช้ประสบการณ์ ความรู้ และความมีเหตุผลแล้ว ยังควรรู้จักวางแผนอย่างเป็นขั้นตอนอย่างเป็นระเบียบด้วย การจำลองความคิดเป็นส่วนหนึ่งในขั้นตอนที่สองของการแก้ปัญหา การจำลองความคิดออกมาในลักษณะเป็นข้อความ หรือเป็นแผนภาพจะช่วยให้สามารถแก้ปัญหาได้ดีโดยเฉพาะอย่างยิ่งปัญหาที่ยุ่งยากซับซ้อน การวางแผนจะเป็นแนวทางในการดำเนินการแก้ปัญหาต่อไป อีกทั้งเป็นการแสดงแบบเพื่อให้ผู้ที่เกี่ยวข้องได้เข้าใจและสามารถปฏิบัติตามในแนวทางเดียวกัน ทั้งนี้ก็ด้วยวัตถุประสงค์อย่างเดียวกับกลุ่มกิจการก่อสร้าง แบบแปลนเหล่านั้น จะอยู่ในรูปลักษณะของการวาดภาพหรือแสดงเครื่องหมายซึ่งเป็นที่เข้าใจกันระหว่างผู้เกี่ยวข้อง แบบแปลนจะต้องจัดทำให้เสร็จก่อนที่จะลงมือก่อสร้าง โดยผ่านการตรวจสอบ ทบทวนและพิจารณาจากผู้เกี่ยวข้องหลายฝ่าย เมื่อเห็นว่าเป็นที่ถูกต้องและพอใจของทุกฝ่ายแล้วจึงก่อสร้างตามแบบนั้น แต่ถ้ายังไม่เป็นที่พอใจ ก็จะพิจารณาแก้ไขแบบแปลนส่วนนั้นๆ เสียก่อนจะได้ไม่ต้องรื้อถอนหรือทุบทิ้งภายหลัง และเมื่อต้องการซ่อมแซมหรือต่อเติมก็นำเอาแบบแปลนเดิมมาตรวจสอบและเพิ่มแบบแปลนในส่วนนั้นได้โดยง่าย การใช้แบบแปลนจึงเป็นสิ่งจำเป็นระหว่างช่างก่อสร้าง ผู้ออกแบบและผู้เกี่ยวข้องอย่างอื่นเป็นอย่างมาก เพราะประหยัดเวลาค่าใช้จ่ายและเข้าใจง่าย เมื่อสรุปรวมแล้วแบบแปลนเหล่านั้นก็คือ ข้อตกลงให้สร้างอาคารของผู้จ้างกับผู้รับจ้างที่อยู่ในรูปแบบกะทัดรัด แทนที่จะเขียนเป็นข้อความที่เป็นลายลักษณ์อักษรอย่างยืดยาว และยังเป็นเครื่องมือให้ช่างใช้ในการก่อสร้างอีกด้วย ขั้นตอนที่สำคัญในการแก้ปัญหา คือ การวางแผน การวางแผนที่ดีจะช่วยให้แก้ปัญหาเป็นไปได้โดยง่าย ผู้ที่สามารถวางแผนในการแก้ปัญหาได้ดีนอกจากจะต้องใช้ประสบการณ์ ความรู้ และความมีเหตุผลแล้ว ยังควรรู้จักวางแผนอย่างเป็นขั้นตอนอย่างเป็นระเบียบด้วย การจำลองความคิดเป็นส่วนหนึ่งในขั้นตอนที่สองของการแก้ปัญหา การจำลองความคิดออกมาในลักษณะเป็นข้อความ หรือเป็นแผนภาพจะช่วยให้สามารถแก้ปัญหาได้ดีโดยเฉพาะอย่างยิ่งปัญหาที่ยุ่งยากซับซ้อน การวางแผนจะเป็นแนวทางในการดำเนินการแก้ปัญหาต่อไป อีกทั้งเป็นการแสดงแบบเพื่อให้ผู้ที่เกี่ยวข้องได้เข้าใจและสามารถปฏิบัติตามในแนวทางเดียวกัน ทั้งนี้ก็ด้วยวัตถุประสงค์อย่างเดียวกับกลุ่มกิจการก่อสร้าง แบบแปลนเหล่านั้น จะอยู่ในรูปลักษณะของการวาดภาพหรือแสดงเครื่องหมายซึ่งเป็นที่เข้าใจกันระหว่างผู้เกี่ยวข้อง แบบแปลนจะต้องจัดทำให้เสร็จก่อนที่จะลงมือก่อสร้าง โดยผ่านการตรวจสอบ ทบทวนและพิจารณาจากผู้เกี่ยวข้องหลายฝ่าย เมื่อเห็นว่าเป็นที่ถูกต้องและพอใจของทุกฝ่ายแล้วจึงก่อสร้างตามแบบนั้น แต่ถ้ายังไม่เป็นที่พอใจ ก็จะพิจารณาแก้ไขแบบแปลนส่วนนั้นๆ เสียก่อนจะได้ไม่ต้องรื้อถอนหรือทุบทิ้งภายหลัง และเมื่อต้องการซ่อมแซมหรือต่อเติมก็นำเอาแบบแปลนเดิมมาตรวจสอบและเพิ่มแบบแปลนในส่วนนั้นได้โดยง่าย การใช้แบบแปลนจึงเป็นสิ่งจำเป็นระหว่างช่างก่อสร้าง ผู้ออกแบบและผู้เกี่ยวข้องอย่างอื่นเป็นอย่างมาก เพราะประหยัดเวลาค่าใช้จ่ายและเข้าใจง่าย เมื่อสรุปรวมแล้วแบบแปลนเหล่านั้นก็คือ ข้อตกลงให้สร้างอาคารของผู้จ้างกับผู้รับจ้างที่อยู่ในรูปแบบกะทัดรัด แทนที่จะเขียนเป็นข้อความที่เป็นลายลักษณ์อักษรอย่างยืดยาว และยังเป็นเครื่องมือให้ช่างใช้ในการก่อสร้างอีกด้วย
 การจำลองความคิดเพื่อวางแผนขั้นตอนในการแก้ปัญหาทางคอมพิวเตอร์นั้น เรียกได้อีกอย่างว่า อัลกอริทึม (Algorithm) หรือขั้นตอนวิธี การจำลองความคิดเพื่อวางแผนขั้นตอนในการแก้ปัญหาทางคอมพิวเตอร์นั้น เรียกได้อีกอย่างว่า อัลกอริทึม (Algorithm) หรือขั้นตอนวิธี
 อัลกอริทึม เป็นลำดับของคำสั่งที่คอมพิวเตอร์จะปฏิบัติตามเพื่อแก้ปัญหาให้กับเรา โดยจะทำคำสั่งเรียงกันตามลำดับก่อนหลัง จะไม่ข้ามขั้นผลลัพธ์ของแต่ละขั้นตอน ผลลัพธ์ที่ได้ของขั้นตอนหนึ่งจะส่งต่อไปยังขั้นตอนถัดไป และส่งต่อกันไปเช่นนี้ตามลำดับขั้น จนถึงคำสั่งสุดท้ายจึงจะได้ผลลัพธ์ที่เสร็จสมบูรณ์เครื่องมือที่ใช้ในการจำลองความคิดมักจะประกอบขึ้นด้วยเครื่องหมายที่แตกต่างกันหลายอย่าง แต่พอสรุปได้เป็น 2 ลักษณะคือ อัลกอริทึม เป็นลำดับของคำสั่งที่คอมพิวเตอร์จะปฏิบัติตามเพื่อแก้ปัญหาให้กับเรา โดยจะทำคำสั่งเรียงกันตามลำดับก่อนหลัง จะไม่ข้ามขั้นผลลัพธ์ของแต่ละขั้นตอน ผลลัพธ์ที่ได้ของขั้นตอนหนึ่งจะส่งต่อไปยังขั้นตอนถัดไป และส่งต่อกันไปเช่นนี้ตามลำดับขั้น จนถึงคำสั่งสุดท้ายจึงจะได้ผลลัพธ์ที่เสร็จสมบูรณ์เครื่องมือที่ใช้ในการจำลองความคิดมักจะประกอบขึ้นด้วยเครื่องหมายที่แตกต่างกันหลายอย่าง แต่พอสรุปได้เป็น 2 ลักษณะคือ
 ข้อความหรือคำบรรยาย เป็นการเขียนเค้าโครงด้วยการบรรยายเป็นภาษามนุษย์ที่ใช้สื่อสารกัน เพื่อให้ทราบถึงขั้นตอนการทำงานของการแก้ปัญหาแต่ละตอน ในบางครั้งอาจใช้คำสั่งของภาษาที่ใช้เขียนโปรแกรมก็ได้ ข้อความหรือคำบรรยาย เป็นการเขียนเค้าโครงด้วยการบรรยายเป็นภาษามนุษย์ที่ใช้สื่อสารกัน เพื่อให้ทราบถึงขั้นตอนการทำงานของการแก้ปัญหาแต่ละตอน ในบางครั้งอาจใช้คำสั่งของภาษาที่ใช้เขียนโปรแกรมก็ได้
 ตัวอย่างที่ 1.4 คำบรรยายแสดงขั้นตอนการเปลี่ยนยางรถเมื่อยางแตกขณะขับรถ ตัวอย่างที่ 1.4 คำบรรยายแสดงขั้นตอนการเปลี่ยนยางรถเมื่อยางแตกขณะขับรถ
 1) จอดรถหลบข้างทาง 1) จอดรถหลบข้างทาง
 2) คลายสกรูยึดล้อ 2) คลายสกรูยึดล้อ
 3) นำแม่แรงออกยกรถ 3) นำแม่แรงออกยกรถ
 4) ถอดล้อออก นำยางอะไหล่มาเปลี่ยน 4) ถอดล้อออก นำยางอะไหล่มาเปลี่ยน
 5) ขันสกรูเข้า เก็บยางที่ชำรุดเพื่อไปซ่อม 5) ขันสกรูเข้า เก็บยางที่ชำรุดเพื่อไปซ่อม
 6) คลายแม่แรง เก็บแม่แรง 6) คลายแม่แรง เก็บแม่แรง
 การเขียนข้อความเพื่อการบรรยายขั้นตอนวิธีในการแก้ปัญหาทางคอมพิวเตอร์ สามารถเรียกอีกอย่างหนึ่งได้ว่า รหัสเทียม (pseudo code) (ศึกษาตัวอย่างเพิ่มเติมได้จากตัวอย่างที่ 1.5-1.7) การเขียนข้อความเพื่อการบรรยายขั้นตอนวิธีในการแก้ปัญหาทางคอมพิวเตอร์ สามารถเรียกอีกอย่างหนึ่งได้ว่า รหัสเทียม (pseudo code) (ศึกษาตัวอย่างเพิ่มเติมได้จากตัวอย่างที่ 1.5-1.7)
 หลักการทั่วไปในการเขียนรหัสเทียม หลักการทั่วไปในการเขียนรหัสเทียม
 1. สัญลักษณ์ที่ใช้ในการดำเนินการทางคณิตศาสตร์ต่างๆ จะถูกใช้งานตามปกติ คือ "+" สำหรับการบวก 1. สัญลักษณ์ที่ใช้ในการดำเนินการทางคณิตศาสตร์ต่างๆ จะถูกใช้งานตามปกติ คือ "+" สำหรับการบวก  "-" สำหรับการลบ"*" สำหรับการคูณ และ "/" สำหรับการหาร "-" สำหรับการลบ"*" สำหรับการคูณ และ "/" สำหรับการหาร
 2. ชื่อข้อมูลแทนจำนวนที่จะถูกดำเนินการ 2. ชื่อข้อมูลแทนจำนวนที่จะถูกดำเนินการ
 3. การกำหนดค่าให้กับชื่อข้อมูล เช่น 3. การกำหนดค่าให้กับชื่อข้อมูล เช่น
 เมื่อเราต้องการกำหนดให้ ข้อมูล pi มีค่าเท่ากับ 3.14 สามารถเขียนได้ด้วยข้อความ pi←3.14 หรือ pi:=3.14 หรือ เมื่อเราต้องการกำหนดให้ ข้อมูล pi มีค่าเท่ากับ 3.14 สามารถเขียนได้ด้วยข้อความ pi←3.14 หรือ pi:=3.14 หรือ
 pi=3.14 pi=3.14
 ในการกำหนดค่าทางคอมพิวเตอร์ด้านซ้ายของเครื่องหมายมักใช้แทน ที่เก็บข้อมูล และ ด้านขวาแทน ในการกำหนดค่าทางคอมพิวเตอร์ด้านซ้ายของเครื่องหมายมักใช้แทน ที่เก็บข้อมูล และ ด้านขวาแทน
 ข้อมูลที่ต้องการนำไปเก็บ (ดังนั้นหากใช้ข้อความว่า 3.14=pi ถือว่าไม่ถูกต้องตาม ความหมายนี้) ข้อมูลที่ต้องการนำไปเก็บ (ดังนั้นหากใช้ข้อความว่า 3.14=pi ถือว่าไม่ถูกต้องตาม ความหมายนี้)
 4. คำสงวนบางคำที่ใช้ในภาษาระดับสูงทั่วไปอาจถูกนำมาใช้ เช่น Read หรือ Enter สำหรับการรับข้อมูลเข้า และ 4. คำสงวนบางคำที่ใช้ในภาษาระดับสูงทั่วไปอาจถูกนำมาใช้ เช่น Read หรือ Enter สำหรับการรับข้อมูลเข้า และ
 Writeหรือ Print สำหรับการแสดงข้อมูลออก Writeหรือ Print สำหรับการแสดงข้อมูลออก
 5.การเพิ่มหรือลดระยะย่อหน้าอย่างเหมาะสมเพื่อแสดงระดับของขั้นตอนการทำงานในโครงสร้างควบคุม 5.การเพิ่มหรือลดระยะย่อหน้าอย่างเหมาะสมเพื่อแสดงระดับของขั้นตอนการทำงานในโครงสร้างควบคุม
 การทำงานในกลุ่มเดียวกัน การทำงานในกลุ่มเดียวกัน
สัญลักษณ์
 เครื่องหมายรูปแบบต่างๆ ซึ่งใช้สำหรับสื่อสารความหมายให้เข้าใจตรงกัน สถาบันมาตรฐานแห่งชาติอเมริกา(The American National Standard Institute, ANSI) ได้กำหนดสัญลักษณ์ไว้เป็นมาตรฐานแล้ว สามารถนำไปใช้ได้ตามความเหมาะสมต่อไป เครื่องหมายรูปแบบต่างๆ ซึ่งใช้สำหรับสื่อสารความหมายให้เข้าใจตรงกัน สถาบันมาตรฐานแห่งชาติอเมริกา(The American National Standard Institute, ANSI) ได้กำหนดสัญลักษณ์ไว้เป็นมาตรฐานแล้ว สามารถนำไปใช้ได้ตามความเหมาะสมต่อไป
 การนำสัญลักษณ์ไปใช้เพื่อแสดงขั้นตอนการทำงานต่างๆ ของงานหรือโปรแกรม รวมถึงแสดงการไหลของข้อมูลในระบบตั้งแต่แรกจนได้ผลลัพธ์ตามต้องการเรียกว่า การเขียนผังงาน(Flowchart) ซึ่งสามารถแบ่งออกได้เป็น 2 แบบคือ การนำสัญลักษณ์ไปใช้เพื่อแสดงขั้นตอนการทำงานต่างๆ ของงานหรือโปรแกรม รวมถึงแสดงการไหลของข้อมูลในระบบตั้งแต่แรกจนได้ผลลัพธ์ตามต้องการเรียกว่า การเขียนผังงาน(Flowchart) ซึ่งสามารถแบ่งออกได้เป็น 2 แบบคือ
 1. ผังงานระบบ(System Flowchart) หมายถึง ผังงานที่แสดงขั้นตอนต่างๆ ในการทำงานของระบบ ช่วยอธิบายลำดับการทำงานของส่วนต่างๆ ในระบบ เช่น การนำข้อมูลเข้า(Input) ถูกเก็บอยู่ที่ใดบ้าง ใช้สื่อบันทึกข้อมูลแบบใด ลักษณะของการประมวลผล ตลอดจนลักษณะของผลลัพธ์(Output) ผังงานระบบจะช่วยอำนวยความสะดวกให้แก่ผู้เขียนโปรแกรมและผู้ที่เกี่ยวข้องที่ต้องการทำความเข้าใจการทำงานของระบบ ตัวอย่างดังรูป 1. ผังงานระบบ(System Flowchart) หมายถึง ผังงานที่แสดงขั้นตอนต่างๆ ในการทำงานของระบบ ช่วยอธิบายลำดับการทำงานของส่วนต่างๆ ในระบบ เช่น การนำข้อมูลเข้า(Input) ถูกเก็บอยู่ที่ใดบ้าง ใช้สื่อบันทึกข้อมูลแบบใด ลักษณะของการประมวลผล ตลอดจนลักษณะของผลลัพธ์(Output) ผังงานระบบจะช่วยอำนวยความสะดวกให้แก่ผู้เขียนโปรแกรมและผู้ที่เกี่ยวข้องที่ต้องการทำความเข้าใจการทำงานของระบบ ตัวอย่างดังรูป
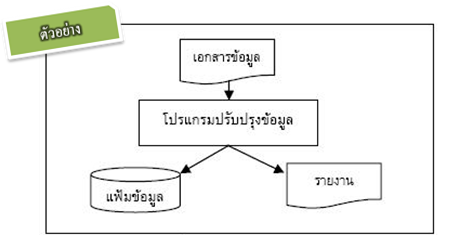
 2. ผังงานโปรแกรม(Program Flowchart) หมายถึง ผังงานที่ใช้ในการแสดงการทำงานของโปรแกรมโดยละเอียดในแต่ละขั้นตอน ผังงานโปรแกรมเป็นสิ่งจำเป็นสำหรับผู้เขียนโปรแกรมเพราะต้องใช้เป็นแนวทางในการเขียนโปรแกรมและเมื่อโปรแกรมเกิด 2. ผังงานโปรแกรม(Program Flowchart) หมายถึง ผังงานที่ใช้ในการแสดงการทำงานของโปรแกรมโดยละเอียดในแต่ละขั้นตอน ผังงานโปรแกรมเป็นสิ่งจำเป็นสำหรับผู้เขียนโปรแกรมเพราะต้องใช้เป็นแนวทางในการเขียนโปรแกรมและเมื่อโปรแกรมเกิด
ข้อผิดพลาดการเข้าไปวิเคราะห์ผังงานโปรแกรมจะทำได้ง่ายกว่าการเข้าไปวิเคราะห์ตัวโปรแกรมโดยตรง
ประโยชน์ของผังงาน
 1. ใช้แทนการจำลองความคิด ช่วยให้เข้าใจลำดับและความสัมพันธ์ระหว่างขั้นตอนในการทำงานต่างๆ 1. ใช้แทนการจำลองความคิด ช่วยให้เข้าใจลำดับและความสัมพันธ์ระหว่างขั้นตอนในการทำงานต่างๆ
 2. ใช้เป็นสื่อกลางในการติดต่อประสานความคิดระหว่างผู้ที่เกี่ยวข้อง เช่น นักวิเคราะห์ระบบ(systems analyst) นักเขียนโปรแกรม(programmer) 2. ใช้เป็นสื่อกลางในการติดต่อประสานความคิดระหว่างผู้ที่เกี่ยวข้อง เช่น นักวิเคราะห์ระบบ(systems analyst) นักเขียนโปรแกรม(programmer)
 3. ช่วยในการทดสอบหรือทบทวนขั้นตอนการทำงาน เพื่อหาข้อผิดพลาด 3. ช่วยในการทดสอบหรือทบทวนขั้นตอนการทำงาน เพื่อหาข้อผิดพลาด
ตารางที่ 1: ความหมายของสัญลักษณ์ที่ใช้ในการเขียนผังงาน




 ตัวอย่างที่ 1.5 การวางแผนไปโรงเรียน ตัวอย่างที่ 1.5 การวางแผนไปโรงเรียน
 การจำลองความคิดด้วยรหัสเทียม การจำลองความคิดด้วยรหัสเทียม
 เริ่มต้น เริ่มต้น
 ตื่นนอน ตื่นนอน
 อาบน้ำแต่งตัว อาบน้ำแต่งตัว
 ไปโรงเรียน ไปโรงเรียน
 จบ จบ
การจำลองความคิดเป็นสัญลักษณ์

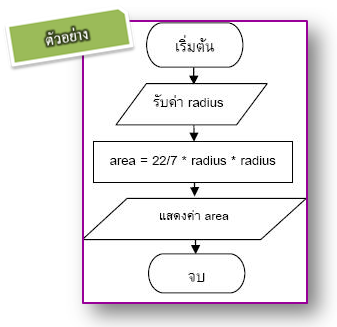
 ตัวอย่างที่ 1.6 การคำนวณพื้นที่รูปวงกลม ตัวอย่างที่ 1.6 การคำนวณพื้นที่รูปวงกลม
 การจำลองความคิดด้วยรหัสเทียม การจำลองความคิดด้วยรหัสเทียม
 เริ่มต้น เริ่มต้น
 รับค่า radius รับค่า radius
 คำนวณพื้นที่ด้วยสูตร area= 22/7 * radius * radius คำนวณพื้นที่ด้วยสูตร area= 22/7 * radius * radius
 แสดงค่า area แสดงค่า area
 จบ จบ
การจำลองความคิดเป็นสัญลักษณ์.
 ตัวอย่างที่ 1.7การจำลองความคิดในการหาผลบวก 1,2,3,4,5,… จนถึง 20 (นั่นคือจะหาค่า 1+2+3+4+5+…+20) ตัวอย่างที่ 1.7การจำลองความคิดในการหาผลบวก 1,2,3,4,5,… จนถึง 20 (นั่นคือจะหาค่า 1+2+3+4+5+…+20)
 การจำลองความคิดด้วยรหัสเทียม การจำลองความคิดด้วยรหัสเทียม
 เริ่มต้น เริ่มต้น
 1. กำหนดให้ N มีค่าเริ่มต้นเป็น 0 1. กำหนดให้ N มีค่าเริ่มต้นเป็น 0
 2. กำหนดให้ K มีค่าเริ่มต้นเป็น 1 2. กำหนดให้ K มีค่าเริ่มต้นเป็น 1
 3. นำค่า K มารวมกับค่า N เดิม ได้ผลลัพธ์เท่าไรเก็บไว้ที่ N 3. นำค่า K มารวมกับค่า N เดิม ได้ผลลัพธ์เท่าไรเก็บไว้ที่ N
 4. นำค่า 1 มารวมกับค่า K เดิม ได้ผลลัพธ์เท่าไรเก็บไว้ที่ K 4. นำค่า 1 มารวมกับค่า K เดิม ได้ผลลัพธ์เท่าไรเก็บไว้ที่ K
 5. เปรียบเทียบค่า K กับ 20 ถ้า K น้อยกว่าหรือเท่ากับ 20 ให้วนกลับไปทำในขั้น 3 และทำคำสั่งถัดลงมาตามลำดับ แต่ถ้า K มากกว่า 20 ให้แสดงคำตอบ 5. เปรียบเทียบค่า K กับ 20 ถ้า K น้อยกว่าหรือเท่ากับ 20 ให้วนกลับไปทำในขั้น 3 และทำคำสั่งถัดลงมาตามลำดับ แต่ถ้า K มากกว่า 20 ให้แสดงคำตอบ
 จบ จบ
การจำลองความคิดเป็นสัญลักษณ์


 จากการศึกษาหลักการขั้นตอนการแก้ปัญหา ในหัวข้อ 1.1 และ 1.2 หลังจากที่เราสามารถวิเคราะห์ปัญหา และสร้างแบบจำลองความคิดเพื่อแสดงขั้นตอนในการแก้ปัญหาแล้ว ขั้นตอนต่อไปคือ การลงมือแก้ปัญหาตามขั้นตอนที่ได้ออกแบบไว้ โดยใช้เครื่องมือช่วยในการแก้ปัญหา ในที่นี้หากเครื่องมือที่นักเรียนเลือก คือ ภาษาคอมพิวเตอร์ซึ่งถือได้ว่าเป็นขั้นตอนหนึ่งที่สำคัญในการแก้ปัญหาด้วยคอมพิวเตอร์ จากการศึกษาหลักการขั้นตอนการแก้ปัญหา ในหัวข้อ 1.1 และ 1.2 หลังจากที่เราสามารถวิเคราะห์ปัญหา และสร้างแบบจำลองความคิดเพื่อแสดงขั้นตอนในการแก้ปัญหาแล้ว ขั้นตอนต่อไปคือ การลงมือแก้ปัญหาตามขั้นตอนที่ได้ออกแบบไว้ โดยใช้เครื่องมือช่วยในการแก้ปัญหา ในที่นี้หากเครื่องมือที่นักเรียนเลือก คือ ภาษาคอมพิวเตอร์ซึ่งถือได้ว่าเป็นขั้นตอนหนึ่งที่สำคัญในการแก้ปัญหาด้วยคอมพิวเตอร์
 การเขียนโปรแกรม (programming) หมายถึง กระบวนการใช้ภาษาคอมพิวเตอร์เพื่อกำหนดโครงสร้างของข้อมูล และกำหนดขั้นตอนวิธีเพื่อใช้แก้ปัญหาตามที่ได้ออกแบบไว้โดยอาศัยหลักเกณฑ์การเขียนโปรแกรมคอมพิวเตอร์ของแต่ละภาษาก่อนการเขียนโปรแกรม ผู้พัฒนาโปรแกรมจะต้องเลือกภาษาที่จะนำมาช่วยใช้งานโดยพิจารณาจากปัจจัยต่างๆ ในการทำงาน เช่น ลักษณะของปัญหา ความถนัดของผู้เขียนโปรแกรม สภาพแวดล้อมในการทำงานของระบบคอมพิวเตอร์ เป็นต้น เนื่องจากในปัจจุบันมีภาษาคอมพิวเตอร์ให้เลือกได้หลายภาษาเช่น ภาษาปาสคาล ภาษาซี ภาษาจาวา ภาษาเดลฟาย เป็นต้น ถึงแม้แต่ละภาษาจะมีรูปแบบและหลักการในการสร้างงานที่แตกต่างกัน แต่ทุกภาษาจะต้องมีโครงสร้างควบคุมหลักทั้ง 3 แบบได้แก่ โครงสร้างแบบลำดับ (sequential structure) โครงสร้างแบบมีทางเลือก (selection structure) และ โครงร้างแบบทำซ้ำ (repetition structure) การเขียนโปรแกรม (programming) หมายถึง กระบวนการใช้ภาษาคอมพิวเตอร์เพื่อกำหนดโครงสร้างของข้อมูล และกำหนดขั้นตอนวิธีเพื่อใช้แก้ปัญหาตามที่ได้ออกแบบไว้โดยอาศัยหลักเกณฑ์การเขียนโปรแกรมคอมพิวเตอร์ของแต่ละภาษาก่อนการเขียนโปรแกรม ผู้พัฒนาโปรแกรมจะต้องเลือกภาษาที่จะนำมาช่วยใช้งานโดยพิจารณาจากปัจจัยต่างๆ ในการทำงาน เช่น ลักษณะของปัญหา ความถนัดของผู้เขียนโปรแกรม สภาพแวดล้อมในการทำงานของระบบคอมพิวเตอร์ เป็นต้น เนื่องจากในปัจจุบันมีภาษาคอมพิวเตอร์ให้เลือกได้หลายภาษาเช่น ภาษาปาสคาล ภาษาซี ภาษาจาวา ภาษาเดลฟาย เป็นต้น ถึงแม้แต่ละภาษาจะมีรูปแบบและหลักการในการสร้างงานที่แตกต่างกัน แต่ทุกภาษาจะต้องมีโครงสร้างควบคุมหลักทั้ง 3 แบบได้แก่ โครงสร้างแบบลำดับ (sequential structure) โครงสร้างแบบมีทางเลือก (selection structure) และ โครงร้างแบบทำซ้ำ (repetition structure)
โครงสร้างแบบลำดับ
 คือโครงสร้างแสดงขั้นตอนการทำงานที่เป็นไปตามลำดับก่อนหลัง และแต่ละขั้นตอนจะถูกประมวลผลเพียงครั้งเดียวเท่านั้น สามารถแสดงการทำงานของโครงสร้างนี้โดยใช้ผังงานได้ดังรูป คือโครงสร้างแสดงขั้นตอนการทำงานที่เป็นไปตามลำดับก่อนหลัง และแต่ละขั้นตอนจะถูกประมวลผลเพียงครั้งเดียวเท่านั้น สามารถแสดงการทำงานของโครงสร้างนี้โดยใช้ผังงานได้ดังรูป

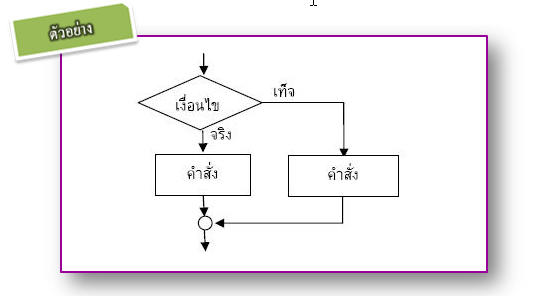
โครงสร้างแบบมีทางเลือก
 คือ โครงสร้างที่มีเงื่อนไข ขั้นตอนการทำงานบางขั้นตอนต้องมีการตัดสินใจเพื่อเลือกวิธีการประมวลผลขั้นต่อไป และจะมีบางขั้นตอนที่ไม่ได้รับการประมวลผล การตัดสินใจอาจมี 2 ทางหรือมากกว่าก็ได้ โครงสร้างที่มีทางเลือกเพียง 2 ทางเราเรียกชื่อว่า โครงสร้างแบบ if…then…else… และโครงสร้างที่มีทางเลือกมากกว่า 2 ทาง เราเรียกชื่อว่าโครงสร้างแบบ case ซึ่งสามารถแสดงการทำงานของโครงสร้างนี้โดยใช้ผังงานดังรูป คือ โครงสร้างที่มีเงื่อนไข ขั้นตอนการทำงานบางขั้นตอนต้องมีการตัดสินใจเพื่อเลือกวิธีการประมวลผลขั้นต่อไป และจะมีบางขั้นตอนที่ไม่ได้รับการประมวลผล การตัดสินใจอาจมี 2 ทางหรือมากกว่าก็ได้ โครงสร้างที่มีทางเลือกเพียง 2 ทางเราเรียกชื่อว่า โครงสร้างแบบ if…then…else… และโครงสร้างที่มีทางเลือกมากกว่า 2 ทาง เราเรียกชื่อว่าโครงสร้างแบบ case ซึ่งสามารถแสดงการทำงานของโครงสร้างนี้โดยใช้ผังงานดังรูป

 ตัวอย่างที่ 1.8 แสดงผังงานที่จำลองขั้นตอนวิธีการเขียนและส่งจดหมายให้อยู่ในรูปของสัญลักษณ์ ตัวอย่างที่ 1.8 แสดงผังงานที่จำลองขั้นตอนวิธีการเขียนและส่งจดหมายให้อยู่ในรูปของสัญลักษณ์

โครงร้างแบบทำซ้ำ
 คือ โครงสร้างที่ขั้นตอนการทำงานบางขั้นตอนได้รับการประมวลผลมากกว่า 1 ครั้ง ทั้งนี้ขึ้นอยู่กับเงื่อนไขบางประการ โครงสร้างแบบทำซ้ำนี้ต้องมีการตัดสินใจในการทำงานซ้ำ และลักษณะการทำงานของโครงสร้างแบบนี้มี 2 ลักษณะ ได้แก่ คือ โครงสร้างที่ขั้นตอนการทำงานบางขั้นตอนได้รับการประมวลผลมากกว่า 1 ครั้ง ทั้งนี้ขึ้นอยู่กับเงื่อนไขบางประการ โครงสร้างแบบทำซ้ำนี้ต้องมีการตัดสินใจในการทำงานซ้ำ และลักษณะการทำงานของโครงสร้างแบบนี้มี 2 ลักษณะ ได้แก่
 แบบที่มีการตรวจสอบเงื่อนไขในการทำซ้ำทุกครั้งก่อนดำเนินการกิจกรรมใดๆ ถ้าเงื่อนไขเป็นจริงจะทำงานซ้ำไปเรื่อยๆ และหยุดเมื่อเงื่อนไขเป็นเท็จ การทำงานลักษณะนี้แบ่งได้เป็น 2 แบบย่อย ได้แก่ การทำซ้ำแบบ for และแบบ while ลักษณะการทำงานของทั้งสองแบบนี้จะเหมือนกัน โดยสำหรับแบบ for นั้นมักใช้กรณีที่ต้องการกำหนดจำนวนรอบการทำงานที่ชัดเจน แบบที่มีการตรวจสอบเงื่อนไขในการทำซ้ำทุกครั้งก่อนดำเนินการกิจกรรมใดๆ ถ้าเงื่อนไขเป็นจริงจะทำงานซ้ำไปเรื่อยๆ และหยุดเมื่อเงื่อนไขเป็นเท็จ การทำงานลักษณะนี้แบ่งได้เป็น 2 แบบย่อย ได้แก่ การทำซ้ำแบบ for และแบบ while ลักษณะการทำงานของทั้งสองแบบนี้จะเหมือนกัน โดยสำหรับแบบ for นั้นมักใช้กรณีที่ต้องการกำหนดจำนวนรอบการทำงานที่ชัดเจน
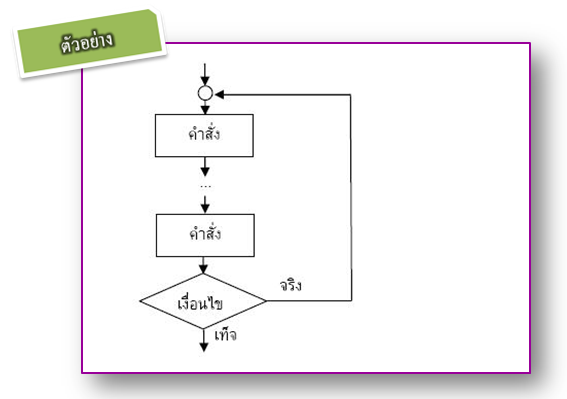
 แบบที่มีการดำเนินการกิจกรรมใดๆ ก่อนจำนวนหนึ่งรอบ แล้วจึงค่อยตรวจสอบเงื่อนไขในการทำซ้ำ ถ้าเงื่อนไขเป็นจริงจะทำงานซ้ำไปเรื่อยๆ และหยุดเมื่อเงื่อนไขเป็นเท็จ เรียกการทำงานแบบนี้ว่า การทำซ้ำแบบ do…while แบบที่มีการดำเนินการกิจกรรมใดๆ ก่อนจำนวนหนึ่งรอบ แล้วจึงค่อยตรวจสอบเงื่อนไขในการทำซ้ำ ถ้าเงื่อนไขเป็นจริงจะทำงานซ้ำไปเรื่อยๆ และหยุดเมื่อเงื่อนไขเป็นเท็จ เรียกการทำงานแบบนี้ว่า การทำซ้ำแบบ do…while
 ผังงานแสดงขั้นตอนการทำงานซ้ำทั้งสองแบบแสดงดังรูป ผังงานแสดงขั้นตอนการทำงานซ้ำทั้งสองแบบแสดงดังรูป

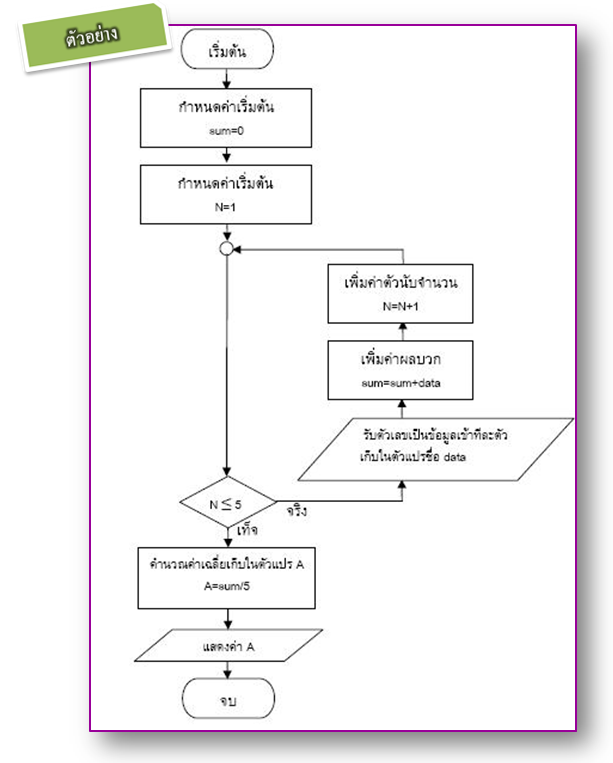
 โครงสร้างควบคุมทั้ง 2 แบบที่กล่าวมาข้างต้นก็คือ ขั้นตอนที่เราใช้ในการแก้ปัญหานั้นเอง พิจารณาตัวอย่างที่ 1.10 เป็นขั้นตอนการเลือกเครื่องมือและการออกแบบขั้นตอนวิธี คือ ขั้นตอนที่ 2 ในหัวข้อ 1.1 เราเลือกสร้างผังงานมาจำลองขั้นตอนวิธีในการหาค่าเฉลี่ยของจำนวน 5 จำนวน จากตัวอย่างที่ 1.2 และในตัวอย่างที่ 1.10 มีการแสดงโครงสร้างควบคุมแบบลำดับและแบบทำซ้ำที่ใช้ในการแก้ปัญหาด้วย โครงสร้างควบคุมทั้ง 2 แบบที่กล่าวมาข้างต้นก็คือ ขั้นตอนที่เราใช้ในการแก้ปัญหานั้นเอง พิจารณาตัวอย่างที่ 1.10 เป็นขั้นตอนการเลือกเครื่องมือและการออกแบบขั้นตอนวิธี คือ ขั้นตอนที่ 2 ในหัวข้อ 1.1 เราเลือกสร้างผังงานมาจำลองขั้นตอนวิธีในการหาค่าเฉลี่ยของจำนวน 5 จำนวน จากตัวอย่างที่ 1.2 และในตัวอย่างที่ 1.10 มีการแสดงโครงสร้างควบคุมแบบลำดับและแบบทำซ้ำที่ใช้ในการแก้ปัญหาด้วย
 ตัวอย่างที่ 1.10 แสดงผังงานที่จำลองขั้นตอนวิธีการหาค่าเฉลี่ยของจำนวนเต็ม 5 จำนวน ให้อยู่ในรูปของสัญลักษณ์ ตัวอย่างที่ 1.10 แสดงผังงานที่จำลองขั้นตอนวิธีการหาค่าเฉลี่ยของจำนวนเต็ม 5 จำนวน ให้อยู่ในรูปของสัญลักษณ์
 |

